Física - Educación Media
6 Dominios | ECEP 2025
1 TIERRA Y UNIVERSO
1.1. Origen y Evolución del Universo
📌 Estructuras cósmicas:
• Vía Láctea: Galaxia espiral, ~200 mil millones de estrellas
• Sistema Solar: Ubicado en brazo de Orión, ~26.000 años luz del centro galáctico
• Superestructuras: Cúmulos galácticos, supercúmulos, filamentos
📌 Fusión nuclear estelar:
Reacción global: 4H → He + energía (fotones + neutrinos). La fusión en el núcleo estelar convierte masa en energía según E = mc².
⭐ Cadena Protón-Protón (Sol)
Estrellas tipo solar (T ≈ 15 millones K):
- 1. H + H → Deuterio + e⁺ + neutrino
- 2. Deuterio + H → ³He + γ
- 3. ³He + ³He → ⁴He + 2H
Resultado: 4 protones → 1 núcleo He + 26.7 MeV
🌟 Ciclo CNO (Estrellas Masivas)
Estrellas masivas (T > 18 millones K):
- • Carbono (C), Nitrógeno (N), Oxígeno (O) actúan como catalizadores
- • Ciclo: ¹²C + 4H → ¹²C + ⁴He + energía
- • CNO se regenera (no se consume)
Más eficiente a altas temperaturas
Relación masa-energía: Por cada kg de H fusionado, ~0.7% de la masa (7g) se convierte en energía pura. El Sol convierte 4 millones de toneladas de masa en energía cada segundo.
📌 Sistema Solar - Clasificación y Datos:
🪨 Planetas Rocosos (Interiores)
Mercurio
- • 0.39 UA
- • 88 días
- • 0 lunas
Venus
- • 0.72 UA
- • 225 días
- • 0 lunas
Tierra
- • 1.00 UA
- • 365 días
- • 1 luna
Marte
- • 1.52 UA
- • 687 días
- • 2 lunas
💨 Gigantes Gaseosos (Exteriores)
Júpiter
- • 5.20 UA
- • 11.8 años
- • 95+ lunas
Saturno
- • 9.54 UA
- • 29.5 años
- • 146+ lunas
Urano
- • 19.2 UA
- • 84 años
- • 27 lunas
Neptuno
- • 30.1 UA
- • 165 años
- • 14 lunas
Nota: 1 UA (Unidad Astronómica) = 149.6 millones de km (distancia Tierra-Sol). Los planetas rocosos son pequeños y densos; los gaseosos son enormes y de baja densidad.
📌 Leyes de Kepler (Mecánica Celeste):
1ª Ley: Órbitas
Los planetas se mueven en elipses con el Sol en uno de los focos. (e = excentricidad).
2ª Ley: Áreas
Barre áreas iguales en tiempos iguales. V_perihelio > V_afelio.
3ª Ley: Periodos
T² ∝ a³
T²/a³ = K (constante)
Cuanto más lejos está el planeta (mayor a), más lento orbita (mayor T).
Fórmula 3ª Ley de Kepler:
T² / a³ = 4π² / (GM)
Ejemplo PAES: Si la distancia de un planeta al Sol se cuadruplica (4a), ¿cómo cambia su periodo?
T² ∝ (4)³ = 64 → T = √64 = 8. El periodo aumenta 8 veces.
📌 El Sol:
• Masa: 1.989×10³⁰ kg (99.86% sistema solar)
• Radio: 696.000 km
• Composición: 73% H, 25% He, 2% otros
👨🏫 Para el Docente: Estrategias Didácticas - Universo y Sistema Solar
💡 Estrategia 1: Modelo a Escala
Actividad: Crear modelo Sistema Solar en patio del colegio usando proporciones reales.
Ejemplo: Si Sol = pelota fútbol (22 cm diámetro) → Tierra = grano arroz (2 mm) a 24 metros de distancia. Permite visualizar vacío espacial (99.99% espacio vacío).
Objetivo: Romper concepción errónea "planetas están cerca entre sí".
❌ Error Común 1: "Fusión nuclear = Fisión nuclear"
Confusión: Estudiantes mezclan conceptos por similitud de nombres.
✅ Clarificación:
- • Fusión: Núcleos LIGEROS se unen (H → He en Sol). Libera MUCHA energía. Requiere T extremas (~15 millones °C).
- • Fisión: Núcleos PESADOS se rompen (U-235 en centrales). Libera energía. Ocurre a T normales con neutrones.
Analogía: Fusión = juntar piezas Lego (difícil, mucha energía). Fisión = romper torre Lego (fácil, neutrones).
❌ Error Común 2: "3ª Ley Kepler solo válida para Sistema Solar"
Realidad: Aplica a CUALQUIER sistema orbital (satélites Tierra, lunas Júpiter, exoplanetas, estrellas binarias).
Ejercicio: Calcular periodo satélite GPS (órbita 20,200 km) usando 3ª Ley Kepler.
🔭 Conexión con Chile: Astronomía Mundial
Contexto local: Chile alberga 70% de infraestructura astronómica mundial (ALMA, VLT, E-ELT en construcción).
Actividad: Visita virtual ALMA (Atacama Large Millimeter Array) - observatorio más poderoso mundo para ondas milimétricas.
Pregunta reflexión: ¿Por qué Atacama es ideal para astronomía? (Cielo despejado 300+ días/año, altitud 5000m, baja humedad, mínima contaminación lumínica).
📊 Evaluación Formativa: Preguntas Clave
- 1. ¿Por qué el Sol no se apaga? (Fusión H continua, combustible para 5 mil millones años más)
- 2. ¿Qué pasaría si Tierra orbitara más cerca del Sol? (↑T, evaporación océanos, efecto invernadero descontrolado como Venus)
- 3. ¿Por qué planetas interiores rocosos y exteriores gaseosos? (Temperatura formación: cerca Sol metales/rocas condensan, lejos hielos/gases)
2 MECÁNICA CLÁSICA
2.1. Cinemática de la Partícula
📌 Marcos de referencia:
Movimiento relativo depende del observador. Velocidad del auto difiere para pasajero (0 m/s) vs peatón (80 km/h).
📌 Movimiento Rectilíneo (1D):
MRU (Velocidad Constante)
a = 0x(t)
v(t)
x(t) = x₀ + v·t
- • Distancias iguales en tiempos iguales.
- • Pendiente gráfico x-t = Velocidad.
- • Área bajo gráfico v-t = Desplazamiento.
MRUV (Aceleración Constante)
a = cte ≠ 0x(t)
v(t)
x(t) = x₀ + v₀t + ½at²
v(t) = v₀ + at
v² = v₀² + 2a(Δx) (Indep. del tiempo)
📌 Movimiento Circular Uniforme (MCU):
r
v
a_c
Velocidad Angular (ω)
ω = Δθ / Δt = 2π / T
Rad/s. Constante en MCU.
Velocidad Tangencial (v)
v = ω·r = 2πr / T
m/s. Magnitud constante, dirección cambia.
Aceleración Centrípeta (a_c)
a_c = v² / r = ω²·r
m/s². Apunta siempre al centro.
Nota: Aunque la rapidez es constante, hay aceleración porque la dirección de la velocidad cambia continuamente.
Ejemplo Resuelto: Lanzamiento Vertical y Caída Libre
2.2. Dinámica de la Partícula
📌 Leyes de Newton (Dinámica):
1ª Ley: Inercia
v = cte
Si F_neta = 0, el objeto mantiene su estado (reposo o MRU). La masa es la medida de la inercia.
2ª Ley: Fundamental
F_neta = m · a
La aceleración es proporcional a la fuerza e inversamente proporcional a la masa.
3ª Ley: Acción-Reacción
F_AB = -F_BA
Fuerzas pares: igual magnitud, dirección opuesta, cuerpos distintos (no se anulan).
📌 Principios de Conservación:
Momentum Lineal (p)
p = mv
Se conserva si F_ext_neta = 0 (ej: choques, explosiones).
Energía Mecánica (E)
E = K + U
Se conserva si solo actúan fuerzas conservativas (peso, elástica). No fricción.
Momentum Angular (L)
L = Iω
Se conserva si Torque_ext_neto = 0 (ej: patinadora cerrando brazos).
📌 Trabajo, Energía, Potencia:
W = F·d·cos(θ) | E_c = ½mv² | P = W/t
Conservación de la Energía Mecánica
2.3. Dinámica del Sólido Rígido
📌 Conceptos Fundamentales de Rotación:
🔄 Torque (τ)
τ = r × F = rF sen(θ)
Análogo a la fuerza en traslación. Causa rotación. Máximo cuando F ⊥ r (θ = 90°).
Unidad: N·m (no confundir con Joule)
⚙️ Momento de Inercia (I)
I = Σ mᵢrᵢ²
Resistencia a cambiar rotación. Análogo a masa en traslación. Depende de distribución de masa.
Unidad: kg·m²
Tabla: Momentos de Inercia de Cuerpos Comunes
| Objeto | Momento de Inercia (I) | Eje de Rotación |
|---|---|---|
| Aro/Anillo delgado | I = MR² | Centro perpendicular al plano |
| Disco/Cilindro sólido | I = ½MR² | Eje central |
| Esfera sólida | I = ⅖MR² | Diámetro |
| Esfera hueca | I = ⅔MR² | Diámetro |
| Varilla delgada | I = 1/12 ML² | Centro perpendicular |
⚡ Energía Cinética Rotacional
Eᶜ_rot = ½Iω²
Análogo a Eᶜ = ½mv². Objeto rodando: Eᶜ_total = ½mv² + ½Iω²
🔄 Momento Angular (L)
L = Iω
Análogo a p = mv. Se conserva si τ_ext = 0.
Relación con lineal: L = r × p = mvr sen(θ)
Ejemplos Prácticos de Rotación de Sólidos Rígidos
⛸️ Ejemplo 1: Patinador Girando
Situación: Patinador artístico gira con brazos extendidos y luego los contrae.
Física: Al contraer brazos, disminuye r → disminuye I. Como L = Iω se conserva (no hay torque externo), ω debe aumentar.
I₁ω₁ = I₂ω₂
Si I₂ < I₁ → ω₂ > ω₁
Conclusión: Gira más rápido con brazos contraídos (conservación L)
🚴 Ejemplo 2: Ruedas de Bicicleta
Situación: Rueda rodando sin deslizar por un plano.
Física: Energía total = traslación + rotación
E_total = ½mv² + ½Iω²
Para rueda: I = MR²
Condición: v = ωR
Aplicación: Al frenar bicicleta, fricción genera torque τ = fR que reduce ω.
Conclusión: Ruedas con menor I aceleran más fácil (bicicletas de carrera)
🎯 Ejemplo 3: Giroscopio
Situación: Trompo o giroscopio precesando (eje cambia dirección lentamente).
Física: Peso genera torque τ = r × mg. Este torque cambia dirección de L, no magnitud.
τ = dL/dt
L perpendicular a τ → precesión
Aplicación: Brújula giroscópica (navegación), estabilización satélites.
Conclusión: Alto L (ω grande) = mayor estabilidad
🚪 Ejemplo Cotidiano: Abrir una Puerta
Aplicar fuerza F en el borde (r máximo) genera mayor torque τ = rF que aplicarla cerca de las bisagras (r pequeño). Por eso las manijas están lejos del eje de rotación. Si aplicas 50 N a 1 m del eje: τ = 50 N·m. La misma fuerza a 0.2 m: τ = 10 N·m (5 veces menor).
2.4. Dinámica de Medios Continuos
📌 Hidrostática:
P = P₀ + ρgh
• Principio Pascal: Presión transmitida íntegramente (prensa hidráulica)
• Principio Arquímedes: Empuje = peso fluido desalojado (flotación)
📌 Capilaridad:
Fenómeno: Ascenso o descenso de líquidos en tubos estrechos debido a tensión superficial y adhesión molecular.
💧 Tensión Superficial
Cohesión entre moléculas del líquido crea "membrana" en superficie. Agua: γ = 0.073 N/m a 20°C.
Ángulo de contacto θ:
• θ < 90° → líquido moja (agua-vidrio)
• θ > 90° → líquido no moja (mercurio-vidrio)
🌱 Aplicaciones
- • Plantas: Xilema (tubos capilares) transporta agua desde raíces a hojas (hasta 100m en árboles altos)
- • Toallas de papel: Absorben agua por capilaridad entre fibras
- • Lámparas de aceite: Mecha transporta combustible
Altura capilar: h = (2γ cos θ) / (ρgr), donde r = radio tubo. A menor radio, mayor ascenso.
🌊 Hidrodinámica: Fluidos en Movimiento
📐 Ecuación de Continuidad (Conservación de Masa)
A₁v₁ = A₂v₂ = Q (caudal constante)
Variables:
- • A = área sección transversal (m²)
- • v = velocidad flujo (m/s)
- • Q = caudal o flujo volumétrico (m³/s)
Interpretación:
En tubo estrecho (A pequeña) el fluido acelera (v grande). En tubo ancho (A grande) el fluido desacelera (v pequeña). Ejemplo: Manguera: tapar parcialmente salida (A↓) → chorro más rápido (v↑).
⚡ Ecuación de Bernoulli (Conservación de Energía)
P + ½ρv² + ρgh = constante
P (Presión estática)
Presión del fluido en reposo. Unidad: Pa (N/m²)
½ρv² (Presión dinámica)
Energía cinética por unidad volumen. Aumenta con velocidad.
ρgh (Presión hidrostática)
Energía potencial por unidad volumen. Aumenta con altura.
💡 Principio: Si velocidad aumenta → presión disminuye (y viceversa). La suma de los 3 términos permanece constante en flujo ideal.
✈️ Aplicación 1: Sustentación de Aviones
Perfil aerodinámico (ala): Aire viaja más rápido por superficie superior (curva más larga) que por inferior (recta más corta).
v_superior > v_inferior
→ P_superior < P_inferior (Bernoulli)
→ Fuerza neta hacia arriba (sustentación)
Resultado: El avión se eleva cuando sustentación > peso.
⚾ Aplicación 2: Efecto Magnus (Pelota Curva)
Situación: Pelota con efecto (spin) en béisbol, fútbol, tenis.
Lado con rotación favorable: v↑ → P↓
Lado con rotación opuesta: v↓ → P↑
→ Diferencia de presión → curva
Ejemplo: Pelota girando hacia derecha: curva hacia derecha (presión menor a ese lado).
Deportistas usan física para controlar trayectorias.
🏠 Aplicación 3: Tubo Venturi
Diseño: Tubo con estrechamiento (constricción) en el medio.
En constricción: A↓ → v↑ (continuidad)
→ P↓ (Bernoulli)
Usos:
- • Carburadores (motores): succión de combustible
- • Medición caudal (flujómetros)
- • Nebulizadores (perfumes, spray)
🚿 Aplicación 4: Tanque con Orificio (Torricelli)
Problema: ¿Con qué velocidad sale agua de orificio en tanque?
Bernoulli en superficie y orificio:
P₀ + 0 + ρgh = P₀ + ½ρv² + 0
→ v = √(2gh) (Teorema Torricelli)
Resultado: Velocidad salida = velocidad caída libre desde altura h.
Ejemplo: Si h = 5m → v = √(2×9.8×5) = 9.9 m/s
⚠️ Para el Docente: Supuestos Flujo Ideal
Las ecuaciones de continuidad y Bernoulli asumen flujo ideal:
- 1. Incompresible: ρ = constante (válido para líquidos, no gases a alta velocidad)
- 2. No viscoso: Sin fricción interna (real: viscosidad causa pérdidas)
- 3. Estacionario: v no cambia con tiempo en cada punto
- 4. Flujo laminar: No turbulento (líneas de corriente suaves)
En realidad: Fluidos tienen viscosidad (miel > agua > aire), hay turbulencias, y se pierde energía. Ecuaciones son aproximaciones útiles para muchos casos prácticos.
🔥 Termodinámica: Calor, Temperatura y Energía
⚛️ Teoría Cinético-Molecular de Gases Ideales
🎯 Supuestos del Gas Ideal:
- 1. Partículas puntiformes (volumen despreciable)
- 2. Sin fuerzas intermoleculares (excepto choques)
- 3. Choques elásticos (conservan energía cinética)
- 4. Movimiento aleatorio continuo
- 5. Temperatura ∝ energía cinética promedio
📐 Ecuación Estado Gas Ideal:
PV = nRT
- • P = presión (Pa)
- • V = volumen (m³)
- • n = moles
- • R = 8.314 J/(mol·K)
- • T = temperatura (K)
También: PV = NkT
(N = moléculas, k = 1.38×10⁻²³ J/K)
Ley de Boyle (T constante)
P₁V₁ = P₂V₂
Presión inversamente proporcional a volumen. Jeringa: comprimir → P↑
Ley de Charles (P constante)
V₁/T₁ = V₂/T₂
Volumen proporcional a temperatura. Globo en frío: V↓
Ley de Gay-Lussac (V constante)
P₁/T₁ = P₂/T₂
Presión proporcional a temperatura. Olla a presión: T↑ → P↑
⚙️ Trabajo Termodinámico y Calor
💪 Trabajo (W)
W = ∫PdV ≈ PΔV (isobárico)
Interpretación:
- • Expansión (ΔV > 0): Gas realiza trabajo (+W), empuja pistón
- • Compresión (ΔV < 0): Trabajo sobre gas (-W), pistón empuja gas
Gráfico P-V: Área bajo curva = |W|
🔥 Calor (Q)
Q = mcΔT (sin cambio fase)
- • m = masa (kg)
- • c = calor específico (J/kg·K)
- • ΔT = cambio temperatura (K)
Cambio de fase: Q = mL
(L = calor latente)
Convención: Q > 0 (sistema absorbe), Q < 0 (sistema libera)
🔬 Las 4 Leyes de la Termodinámica
0️⃣ Ley Cero (Equilibrio Térmico)
Enunciado: Si A en equilibrio térmico con B, y B con C, entonces A en equilibrio con C.
Importancia: Fundamenta el concepto de temperatura. Dos cuerpos en equilibrio térmico tienen misma temperatura.
Aplicación: Termómetros. Termómetro alcanza equilibrio con cuerpo → miden misma T.
1️⃣ Primera Ley (Conservación Energía)
ΔU = Q - W
Variables:
- • ΔU = cambio energía interna
- • Q = calor absorbido (+ entrada, - salida)
- • W = trabajo realizado por sistema (+ expansión, - compresión)
Interpretación: Energía se conserva. Calor aportado = aumento energía interna + trabajo realizado.
2️⃣ Segunda Ley (Entropía)
Enunciados equivalentes:
- • Clausius: Calor no fluye espontáneamente de frío a caliente
- • Kelvin-Planck: Imposible máquina térmica 100% eficiente (η < 1)
- • Entropía: ΔS_universo ≥ 0 (procesos irreversibles aumentan desorden)
Consecuencia: Procesos naturales tienen dirección (flecha del tiempo). Energía se degrada (dispersa).
3️⃣ Tercera Ley (Cero Absoluto)
Enunciado: Imposible alcanzar T = 0 K (cero absoluto) en número finito de pasos.
Significado: A T = 0 K:
- • Entropía = 0 (cristal perfecto)
- • Movimiento molecular cesa (mínima energía cuántica)
- • Se puede acercar (récord: 10⁻¹⁰ K) pero nunca llegar
Aplicación: Límite fundamental para refrigeración. Superconductores requieren T cercanas a 0 K.
🔄 Procesos Termodinámicos Especiales
| Proceso | Constante | Primera Ley (ΔU = Q - W) | Ejemplo |
|---|---|---|---|
| Isotérmico | T (temperatura) | ΔU = 0 → Q = W | Expansión lenta gas (baño térmico) |
| Isobárico | P (presión) | Q = ΔU + PΔV | Ebullición agua (P_atm constante) |
| Isocórico (Isovolumétrico) | V (volumen) | W = 0 → ΔU = Q | Calentar gas en recipiente rígido |
| Adiabático | Q = 0 (aislado) | ΔU = -W | Compresión rápida (bomba inflado) |
👨🏫 Para el Docente: Concepciones Erróneas Comunes
- ❌ Error: "Calor y temperatura son lo mismo"
✅ Correcto: Calor es transferencia de energía (J). Temperatura es medida de energía cinética promedio (K). Un iceberg tiene más calor que un fósforo encendido (mayor masa), pero menor temperatura. - ❌ Error: "Los objetos fríos no tienen calor"
✅ Correcto: Todos los objetos sobre 0 K tienen energía térmica. "Frío" es relativo (menos energía que entorno). - ❌ Error: "Máquina perpetua viola primera ley"
✅ Correcto: Viola segunda ley. Primera ley permite ciclo sin pérdida energía, pero segunda ley impide eficiencia 100% (siempre hay entropía).
📌 Oscilaciones - Movimiento Armónico Simple (MAS):
🔄 Péndulo Simple
T = 2π√(L/g)
Variables:
- • T = periodo (s)
- • L = longitud cuerda (m)
- • g = aceleración gravedad (9.8 m/s²)
Nota: T independiente de masa y amplitud (si ángulo < 15°)
🪀 Resorte (MAS)
T = 2π√(m/k)
Variables:
- • m = masa (kg)
- • k = constante elástica (N/m)
Fuerza restauradora: F = -kx (Ley Hooke)
Características del MAS:
- • Movimiento periódico (se repite en tiempo T)
- • Fuerza restauradora proporcional a desplazamiento: F = -kx
- • Energía mecánica conservada: E = ½kA² (A = amplitud)
- • Velocidad máxima en equilibrio (x = 0), velocidad cero en extremos (x = ±A)
Ejemplos cotidianos: reloj de péndulo, suspensión auto (amortiguadores), puentes (evitar resonancia), instrumentos musicales (cuerdas, membranas).
📌 Ondas mecánicas:
v = λf
Variables: v = velocidad propagación (m/s), λ = longitud onda (m), f = frecuencia (Hz)
Tipos: Transversales (cuerdas, luz), longitudinales (sonido, resorte). Requieren medio material (excepto electromagnéticas). Sonido en aire: v ≈ 343 m/s (20°C).
3 ELECTROMAGNETISMO Y ÓPTICA
3.1. Electrostática
📌 Campo y potencial eléctrico:
E = F/q | V = W/q | E = kQ/r²
Relación Campo-Potencial:
E = -∇V = -dV/dr
Interpretación: El campo eléctrico es el gradiente negativo del potencial. Las cargas se mueven de mayor a menor potencial (campo apunta hacia potencial decreciente).
- • Trabajo: W = q(V₁ - V₂) = qΔV
- • Campo uniforme: E = ΔV/d (entre placas paralelas)
- • Diferencia clave: E es vectorial (dirección), V es escalar (magnitud)
Rayos en tormentas: Descarga entre nube-tierra por diferencia de potencial extrema (~100 MV). Campo eléctrico supera rigidez dieléctrica del aire (3×10⁶ V/m), ionizando moléculas y creando canal conductor.
3.2. Corriente Eléctrica
📌 Circuitos Eléctricos (Ley de Ohm):
Circuito en Serie
- • Corriente (I): Igual en todo el circuito.
- • Voltaje (V): Se reparte (V_total = V1 + V2).
- • R_eq: R1 + R2 (Aumenta resistencia total).
- • Si falla uno, falla todo.
Circuito en Paralelo
- • Voltaje (V): Igual en cada rama.
- • Corriente (I): Se reparte (I_total = I1 + I2).
- • R_eq: (1/R1 + 1/R2)⁻¹ (Disminuye resistencia total).
- • Independencia de componentes.
V = I · R (Ley de Ohm)
📌 Efecto Joule:
P = VI = I²R = V²/R | E = Pt
Energía eléctrica → calor. Aplicaciones: calefactores, tostadores, ampolletas incandescentes.
3.3. Fenómenos Ópticos y Electromagnéticos
📌 Propiedades magnéticas de la materia:
🧲 Ferromagnetismo
Fe, Co, Ni, Gd. Atracción fuerte, imanes permanentes. Dominios magnéticos se alinean. Pierde magnetismo sobre Temp. Curie.
⬆️ Paramagnetismo
Al, Pt, O₂. Atracción débil. Electrones desapareados. Magnetización desaparece sin campo externo.
⬇️ Diamagnetismo
Cu, Ag, Au, H₂O. Repulsión muy débil. Todos los materiales tienen componente diamagnética. Electrones apareados.
❄️ Superconductividad
R = 0 a bajas T (
📌 Dispositivos electromagnéticos:
🔌 Generador
Principio: Movimiento → Electricidad
Ley Faraday (inducción): ε = -dΦ_B/dt. Cambio flujo magnético induce voltaje. Espira rotando en campo B genera corriente alterna.
⚙️ Motor
Principio: Electricidad → Movimiento
Fuerza Lorentz: F = qv×B. Corriente en conductor dentro de B experimenta fuerza. Espira con corriente rota en campo magnético.
🔄 Transformador (AC solamente)
Función: Aumentar o disminuir voltaje AC mediante inducción electromagnética.
V₁/V₂ = N₁/N₂
I₁/I₂ = N₂/N₁
Variables:
- • V = voltaje (primario/secundario)
- • N = número de espiras (vueltas)
- • I = corriente
Tipos:
- • Elevador: N₂ > N₁ → V₂ > V₁ (transmisión eléctrica: 220V → 500kV)
- • Reductor: N₂ < N₁ → V₂ < V₁ (cargadores: 220V → 5V)
Conservación energía: P₁ = P₂ (ideal)
V₁I₁ = V₂I₂
Aplicación: Torres alta tensión reducen pérdidas por efecto Joule (P_pérdida = I²R). Alto V → bajo I → menores pérdidas.
🧲 Electroimán
Construcción: Bobina (solenoide) enrollada alrededor de núcleo ferromagnético (Fe). Corriente eléctrica genera campo magnético.
B = μ₀nI (n = espiras/longitud)
Ventaja vs imán permanente: Campo controlable (encender/apagar, intensidad ajustable).
Aplicaciones: Grúas industriales (chatarra), timbres, relés, altavoces, MRI (resonancia magnética), aceleradores partículas.
📌 Espectro electromagnético:
Todas viajan a c = 3×10⁸ m/s en vacío. Orden (menor a mayor frecuencia):
Radio → Microondas → Infrarrojo → Visible → Ultravioleta → Rayos X → Rayos γ
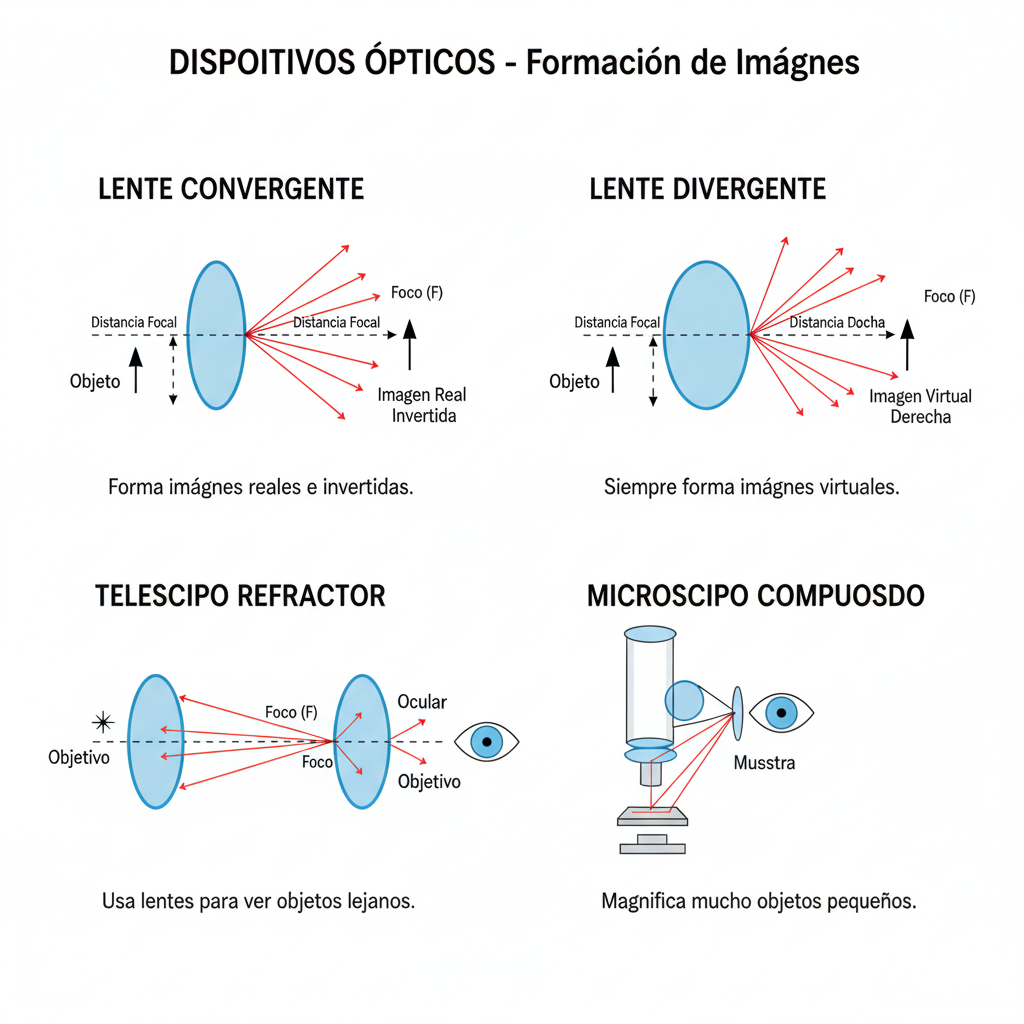
📌 Óptica - Dispositivos y Formación de Imágenes:
🪞 Espejos
Ley reflexión: θᵢ = θᵣ (ángulo incidencia = reflexión)
- • Plano: Imagen virtual, mismo tamaño, invertida izq-der
- • Cóncavo (convergente): Foco real, puede formar imágenes reales o virtuales
- • Convexo (divergente): Foco virtual, siempre imagen virtual reducida
1/f = 1/dₒ + 1/dᵢ
Aumento: m = -dᵢ/dₒ
🔍 Lentes
Ley Snell (refracción): n₁ sen(θ₁) = n₂ sen(θ₂)
- • Convergente (convexa): Enfoca luz, f > 0. Lupa, corrección hipermetropía
- • Divergente (cóncava): Dispersa luz, f < 0. Corrección miopía
1/f = 1/dₒ + 1/dᵢ
Potencia: P = 1/f (dioptrías)
Convención signos: dᵢ > 0 (real), dᵢ < 0 (virtual)
🔭 Instrumentos Ópticos
🔭 Telescopios
| Tipo | Objetivo | Ventaja |
|---|---|---|
| Refracción | Lente | Simple, portable |
| Reflexión (Newton) | Espejo | Sin aberración cromática, + grandes |
Función: Objetivo recoge luz (imagen real pequeña) + Ocular amplía (lupa). Aumento = f_objetivo / f_ocular
🔬 Microscopio Compuesto
Componentes:
- • Objetivo: Lente convergente cerca del objeto (f corta). Forma imagen real aumentada invertida.
- • Ocular: Lupa que amplía imagen del objetivo. Imagen virtual final muy aumentada.
Aumento_total = m_obj × m_oc
Típico: 40× (objetivo) × 10× (ocular) = 400× total
🔭 Binoculares (Prismáticos)
Dos telescopios refractores en paralelo. Prismas internos (reflexión total) invierten imagen y compactan diseño. Notación 10×50: aumento 10×, objetivo 50mm diámetro. Mayor diámetro → más luz → mejor visión nocturna.
🌈 Modelos de la Luz - Dualidad Onda-Partícula
📡 Modelo Ondulatorio
- • Explica: Interferencia, difracción, polarización
- • Experimento Young (doble rendija)
- • λ visible: 400-700 nm
⚛️ Modelo Corpuscular
- • Explica: Efecto fotoeléctrico, Compton
- • Fotones: E = hf (cuantos energía)
- • Einstein (1905): Premio Nobel 1921
Dualidad: Luz exhibe propiedades de onda Y partícula según experimento. Base mecánica cuántica moderna.
👨🏫 Para el Docente: Estrategias Electromagnetismo y Óptica
❌ Error Conceptual: "Corriente eléctrica = flujo de electrones a velocidad de la luz"
Realidad: Electrones se mueven muy lento (~mm/s velocidad de deriva), pero señal eléctrica viaja rápido (~c/2 en cables).
✅ Analogía: Manguera llena de agua. Al abrir llave (un extremo), agua sale inmediato (otro extremo), pero moléculas individuales avanzan lento. Presión se transmite rápido, no las moléculas.
💡 Experimento Demostración: Ley de Ohm con Multímetro
Materiales: Fuente variable, resistencias conocidas (100Ω, 220Ω, 470Ω), multímetros digital.
Procedimiento: Variar voltaje (2V, 4V, 6V, 8V, 10V), medir corriente, graficar V vs I.
Resultado esperado: Gráfico lineal (pendiente = R). Calcular R experimental, comparar con valor nominal.
⚠️ Cuidado: No exceder potencia máxima resistor (P = V²/R). Resistor 1/4W a 10V en 100Ω → P = 1W (se sobrecalienta).
🔍 Concepto Difícil: Diferencia Campo Eléctrico vs Potencial
Confusión frecuente: Estudiantes no distinguen E (vectorial, N/C) de V (escalar, V).
✅ Clarificación:
- • Potencial V: "Altura energética" (como altura geográfica). Escalar.
- • Campo E: "Pendiente del terreno" (dirección descenso más pronunciado). Vector.
- • Relación: E = -∇V (campo apunta hacia potencial decreciente)
Analogía: Mapa topográfico. Curvas nivel = líneas equipotenciales. Pendiente (∇) = campo eléctrico.
🌈 Actividad Integradora: Espectro Electromagnético
Desafío: Ordenar usos tecnológicos por tipo de radiación (radio → microondas → IR → visible → UV → rayos X → gamma).
Ejemplos: WiFi (microondas 2.4 GHz), control remoto (IR), esterilización médica (UV-C), radiografías (rayos X), radioterapia cáncer (gamma).
Objetivo: Conectar física abstracta con tecnología cotidiana.
4 NÚCLEO ATÓMICO
📌 Las 4 Fuerzas Fundamentales:
1. Gravitatoria
Más débil- • Mediador: Gravitón (hipotético).
- • Alcance: Infinito (∝ 1/r²).
- • Efecto: Solo atracción. Domina a gran escala (planetas, galaxias).
- • Magnitud: 1 (Referencia).
2. Electromagnética
Fuerte- • Mediador: Fotón (γ).
- • Alcance: Infinito (∝ 1/r²).
- • Efecto: Atracción/Repulsión. Enlaces químicos, luz, electricidad.
- • Magnitud: 10³⁶ veces gravedad.
3. Nuclear Débil
Corto alcance- • Mediador: Bosones W⁺, W⁻, Z⁰.
- • Alcance: Subatómico (~10⁻¹⁸ m).
- • Efecto: Desintegración beta (radiactividad), fusión solar.
- • Magnitud: 10²⁵ veces gravedad.
4. Nuclear Fuerte
La más fuerte- • Mediador: Gluones.
- • Alcance: Núcleo (~10⁻¹⁵ m).
- • Efecto: Mantiene unidos protones y neutrones (vence repulsión eléctrica).
- • Magnitud: 10³⁸ veces gravedad.
🌌 Comparación de Alcances:
- • Infinito: Gravedad y electromagnetismo actúan a cualquier distancia (aunque debilitan con r²)
- • Corto: Fuerte y débil solo dentro del núcleo atómico
- • Por eso la gravedad domina escala cósmica (masas neutras)
⚛️ Modelo Estándar:
Estas 4 fuerzas + partículas fundamentales (quarks, leptones) explican toda materia observable. Desafío actual: Unificar gravedad (Relatividad General) con otras 3 fuerzas (Mecánica Cuántica) en Teoría del Todo.
5 RAZONAMIENTO CIENTÍFICO
🔬 Variables y diseño:
- • Independiente: Manipulada por experimentador
- • Dependiente: Medida (responde a cambios)
- • Controladas: Mantenidas constantes
- • Hipótesis verificables con datos empíricos
📊 Análisis:
- • Interpretar datos (tablas, gráficos)
- • Conclusiones válidas basadas en evidencia
- • Argumentos científicos coherentes
- • Identificar mejoras experimentales
Ejemplos de Diseños Experimentales en Física
🌍 Ejemplo 1: Medición de g (Gravedad)
Pregunta de Investigación:
¿Cómo varía el tiempo de caída con la altura en caída libre?
Variables:
- • Independiente: Altura h (m)
- • Dependiente: Tiempo caída t (s)
- • Controladas: Masa objeto, forma (esfera), resistencia aire (despreciable)
Diseño Experimental:
- 1. Soltar esfera desde alturas: 1m, 2m, 3m, 4m, 5m
- 2. Medir tiempo con cronómetro (3 repeticiones)
- 3. Promediar resultados
- 4. Graficar h vs t² (relación lineal)
- 5. Calcular g de pendiente: h = ½gt²
Mejoras Propuestas:
- ✓ Usar fotopuertas en vez de cronómetro manual (error humano ~0.2s)
- ✓ Realizar experimento en tubo de vacío (eliminar resistencia aire)
- ✓ Usar cámara alta velocidad para análisis cuadro por cuadro
- ✓ Aumentar alturas (mayor rango datos)
⚡ Ejemplo 2: Ley de Ohm (V = IR)
Pregunta de Investigación:
¿Es la corriente proporcional al voltaje en un conductor óhmico?
Variables:
- • Independiente: Voltaje V (V)
- • Dependiente: Corriente I (A)
- • Controladas: Resistencia (100Ω), temperatura, conexiones
Diseño Experimental:
- 1. Circuito: Fuente variable + resistor + multímetros (V e I)
- 2. Variar voltaje: 2V, 4V, 6V, 8V, 10V
- 3. Medir corriente en cada caso
- 4. Graficar V vs I (esperado: lineal)
- 5. Calcular R de pendiente: R = V/I
Mejoras Propuestas:
- ✓ Repetir con diferentes resistencias (47Ω, 220Ω, 1kΩ)
- ✓ Usar amperímetro digital (mayor precisión que analógico)
- ✓ Disipar calor (resistor no se caliente y cambie R)
- ✓ Comparar con resistor no óhmico (LED, diodo) para contraste
⏱️ Ejemplo 3: Péndulo Simple (T vs L)
Pregunta de Investigación:
¿Cómo depende el periodo de oscilación de la longitud del péndulo?
Variables:
- • Independiente: Longitud L (m)
- • Dependiente: Periodo T (s)
- • Controladas: Masa, amplitud (ángulo < 15°), lugar (g constante)
Diseño Experimental:
- 1. Péndulo con longitudes: 0.25m, 0.50m, 0.75m, 1.00m
- 2. Soltar desde ángulo pequeño (~10°)
- 3. Medir tiempo de 10 oscilaciones completas
- 4. T = t_total / 10 (periodo individual)
- 5. Graficar T² vs L (lineal: T² ∝ L)
Mejoras Propuestas:
- ✓ Promediar 10 oscilaciones (reduce error cronómetro)
- ✓ Mantener ángulo < 15° (garantía MAS, sinθ ≈ θ)
- ✓ Usar sensor fotoceléctrico (detección automática)
- ✓ Verificar independencia de masa (cambiar peso)
💡 Conclusiones de Diseño Experimental:
- • Variables claras: Identificar qué cambia (indep.), qué se mide (dep.), qué se mantiene (control)
- • Repeticiones: Promediar reduce error aleatorio
- • Gráficos: Visualizar relaciones (lineal, cuadrática, inversa)
- • Mejoras: Tecnología (sensores), control ambiental, mayor rango datos
6 ENSEÑANZA-APRENDIZAJE EN FÍSICA
👩🏫 Estrategias
- • Metodologías activas
- • Analogías físicas
- • Recursos didácticos
- • Énfasis CTS
📚 Aprendizaje
- • Conocimientos previos
- • Preconceptos erróneos
- • Dificultades comunes
✅ Evaluación
- • Indicadores claros
- • Instrumentos adecuados
- • Retroalimentación
Caso Pedagógico 1: "Fuerza Necesaria para Mantener Movimiento"
🎯 Situación:
Un estudiante afirma: "Para que un auto mantenga velocidad constante de 80 km/h, el motor debe aplicar fuerza constante en dirección del movimiento. Si se apaga el motor, el auto se detiene porque no hay fuerza."
❌ Preconcepto Detectado (Física Aristotélica):
Error conceptual: Creer que se necesita fuerza constante para mantener movimiento uniforme. Esta es una visión aristotélica (pre-newtoniana) que confunde fuerza con velocidad en lugar de fuerza con aceleración.
- • Confusión: Fuerza → Velocidad (incorrecto) vs Fuerza → Aceleración (correcto)
- • Ignorancia de fricción como fuerza que se opone al movimiento
- • No distingue entre mundo ideal (sin fricción) y real (con fricción)
✅ Estrategia Didáctica:
1. Experimento Mental: Disco sobre Colchón de Aire
Situación ideal: Disco de hockey sobre mesa con colchón de aire (fricción ≈ 0).
Observación: Al darle impulso inicial, el disco continúa moviéndose con velocidad constante SIN aplicar fuerza adicional.
Pregunta clave: "¿Por qué el disco sigue moviéndose si no hay fuerza actuando?"
2. Análisis de Fuerzas (Diagrama de Cuerpo Libre):
Auto con Velocidad Constante (80 km/h)
- • F_motor (adelante) = 500 N
- • F_fricción + F_aire (atrás) = 500 N
- • F_neta = 0 N → a = 0 → v constante ✓
1ª Ley Newton: Si F_neta = 0, v = constante (MRU)
Auto Apagado (Motor OFF)
- • F_motor = 0 N
- • F_fricción + F_aire = 500 N (atrás)
- • F_neta = -500 N → a < 0 → desacelera
Se detiene por fricción, NO por "ausencia de fuerza motriz"
3. Tabla Comparativa de Escenarios:
| Situación | Fuerzas | F_neta | Movimiento |
|---|---|---|---|
| Espacio exterior (sin fricción) | Ninguna | 0 | MRU eterno (1ª Ley) |
| Auto en autopista (v constante) | Motor = Fricción | 0 | MRU (equilibrio dinámico) |
| Auto acelerando | Motor > Fricción | > 0 | MRUV (a > 0) |
| Auto frenando (motor OFF) | Solo fricción | < 0 | MRUV (a < 0) |
4. Concepto Clave Newtoniano:
F_neta = ma
- • Si F_neta = 0 → a = 0 → v constante (objeto sigue moviéndose o en reposo)
- • Si F_neta ≠ 0 → a ≠ 0 → v cambia (acelera o desacelera)
- • Inercia: Tendencia a mantener estado de movimiento sin fuerza externa
📊 Evaluación del Aprendizaje:
Pregunta: "Un satélite orbita la Tierra a velocidad constante de 7.8 km/s. ¿Necesita motores encendidos constantemente para mantener esta velocidad?"
Respuesta esperada: No. En el vacío del espacio no hay fricción atmosférica. La única fuerza es la gravedad (centrípeta), que cambia DIRECCIÓN de velocidad (órbita circular) pero no su MAGNITUD. El satélite mantiene velocidad tangencial constante por inercia (1ª Ley Newton). Solo necesita motores para correcciones ocasionales.
Caso Pedagógico 2: "Peso y Masa Son lo Mismo"
🎯 Situación:
Un estudiante dice: "Mi peso es 60 kg" o "En la Luna peso 10 kg porque la gravedad es menor." Al preguntarle qué unidad usar para el peso, responde "kilogramos".
❌ Preconcepto Detectado:
Confusión conceptual: No distinguir entre masa (cantidad de materia) y peso (fuerza gravitatoria). Usar kg para ambas magnitudes.
- • Creer que masa y peso son sinónimos
- • Usar kg (unidad de masa) para expresar peso (debería ser N)
- • Pensar que masa cambia con ubicación (Tierra, Luna, espacio)
✅ Estrategia Didáctica:
1. Definiciones Contrastadas:
⚛️ Masa (m)
- • Definición: Cantidad de materia en un objeto
- • Magnitud: Escalar
- • Unidad SI: kilogramo (kg)
- • Propiedad: Intrínseca (NO cambia con ubicación)
- • Instrumento: Balanza (compara masas)
⬇️ Peso (W o P)
- • Definición: Fuerza gravitatoria sobre un objeto
- • Magnitud: Vectorial (dirección: hacia centro Tierra)
- • Unidad SI: Newton (N)
- • Propiedad: Extrínseca (cambia con g)
- • Instrumento: Dinamómetro (mide fuerza)
2. Relación Matemática:
W = mg
- • m: masa (kg) - constante
- • g: aceleración gravedad (m/s²) - variable según ubicación
- • W: peso (N) - depende de g
3. Tabla Comparativa por Ubicación:
| Ubicación | g (m/s²) | Masa (kg) | Peso (N) | Relación con Tierra |
|---|---|---|---|---|
| 🌍 Tierra | 9.8 | 60 | 588 N | 1 (referencia) |
| 🌙 Luna | 1.6 | 60 (mismo) | 96 N | 1/6 Tierra |
| 🪐 Júpiter | 24.8 | 60 (mismo) | 1,488 N | 2.5 × Tierra |
| 🚀 Espacio (órbita) | ≈0 (ingravidez) | 60 (mismo) | ≈0 N | Sin peso aparente |
Conclusión: Masa NO cambia, peso SÍ cambia según g del lugar.
4. Experimento Mental Luna:
Pregunta guía: "Si llevas una roca de 6 kg de la Tierra a la Luna:"
- • ¿Cuántos kg tiene en la Luna? → 6 kg (masa no cambia)
- • ¿Cuántos Newtons pesa en Tierra? → W = 6 kg × 9.8 m/s² = 58.8 N
- • ¿Cuántos Newtons pesa en Luna? → W = 6 kg × 1.6 m/s² = 9.6 N
- • ¿Es más fácil levantarla en la Luna? → Sí (menos peso), pero igual de difícil acelerarla horizontalmente (misma masa = misma inercia)
📊 Evaluación del Aprendizaje:
Pregunta: "Un astronauta tiene masa de 80 kg en la Tierra. ¿Cuál es su masa y peso en la Luna (g_Luna = 1.6 m/s²)? Expresa con unidades correctas."
Respuesta esperada:
- • Masa en Luna: 80 kg (la masa es intrínseca, NO cambia)
- • Peso en Tierra: W = mg = 80 kg × 9.8 m/s² = 784 N
- • Peso en Luna: W = mg = 80 kg × 1.6 m/s² = 128 N
- • Conclusión: Misma masa (80 kg), diferente peso (784 N → 128 N)
Error común a evitar: Decir "peso 80 kg en Tierra y 13 kg en Luna" (confunde unidades).
Caso Pedagógico: "Confusión Velocidad-Aceleración"
🎯 Situación:
Un estudiante afirma: "Un auto que va a 120 km/h tiene más aceleración que uno que va a 60 km/h."
❌ Preconcepto Detectado:
Confusión conceptual entre velocidad (magnitud del movimiento) y aceleración (variación de la velocidad). El estudiante asocia "ir rápido" con "acelerar".
✅ Estrategia Didáctica:
1. Analogía del Ascensor:
- • Velocidad: "¿A qué piso voy?" (posición cambiando en el tiempo)
- • Aceleración: "¿Siento presión en los pies?" (solo al arrancar/frenar)
- • Clave: Puedes sentir aceleración (fuerza) incluso con velocidad = 0 (al arrancar)
2. Tabla Comparativa de Escenarios:
| Escenario | Velocidad (v) | Aceleración (a) | ¿Qué sientes? |
|---|---|---|---|
| Auto en autopista | 120 km/h (constante) | a = 0 | Nada, vas suave |
| Auto acelerando | 60 → 80 km/h | a > 0 | Te hundes en el asiento |
| Auto frenando | 100 → 40 km/h | a < 0 | Te vas hacia adelante |
| Parado arrancando | 0 → 20 km/h | a > 0 (MÁXIMA) | Aceleración SIN velocidad inicial |
3. Experimento con Gráficos v-t:
Dibujar dos gráficos:
• Gráfico A: Línea horizontal en v = 120 km/h → Pendiente = 0 → a = 0
• Gráfico B: Línea inclinada desde 0 a 60 km/h → Pendiente > 0 → a > 0
Conclusión: El gráfico B tiene aceleración aunque alcanza menor velocidad.
4. Definición Matemática:
a = Δv/Δt = (v_final - v_inicial)/tiempo
Ejemplo 1: Auto en autopista → Δv = 0 → a = 0/t = 0 m/s²
Ejemplo 2: Auto arrancando → Δv = 20 km/h → a ≠ 0
📊 Evaluación del Aprendizaje:
Pregunta de seguimiento: "Un paracaidista cae con velocidad constante de 50 m/s (velocidad terminal). ¿Cuál es su aceleración?"
Respuesta esperada: a = 0 m/s² porque la velocidad es constante (no cambia), aunque va muy rápido. Las fuerzas están balanceadas: peso = resistencia del aire.